গণিতের চারটি মৌলিক প্রক্রিয়া হলো যোগ, বিয়োগ, গুণ ও ভাগ। বিয়োগ হচ্ছে যোগের বিপরীত প্রক্রিয়া আর ভাগ হচ্ছে গুণের বিপরীত প্রক্রিয়া। পাটিগণিতে কেবল ধনাত্মক চিহ্নযুক্ত সংখ্যা ব্যবহার করা হয়। কিন্তু বীজগণিতে ধনাত্মক ও ঋণাত্মক উভয় চিহ্নযুক্ত সংখ্যা এবং সংখ্যাসূচক প্রতীকও ব্যবহার করা হয়। আমরা ষষ্ঠ শ্রেণিতে চিহ্নযুক্ত রাশির যোগ-বিয়োগ এবং বীজগণিতীয় রাশির যোগ ও বিয়োগ সম্বন্ধে ধারণা পেয়েছি। এ অধ্যায়ে চিহ্নযুক্ত রাশির গুণ ও ভাগ এবং বীজগণিতীয় রাশির গুণ ও ভাগ প্রক্রিয়া সম্বন্ধে আলোচনা করা হয়েছে।
অধ্যায় শেষে শিক্ষার্থীরা -
গুণের বিনিময়বিধি
আমরা জানি,
2 3 = 6 আবার 3 2 = 6
2 3 = 3 2 যা গুণের বিনিময়বিধি।
| a, b যেকোনো দুটি বীজগণিতীয় রাশি হলে, ab = ba অর্থাৎ, গুণ্য ও গুণকের স্থান বিনিময় করলে, গুণফলের কোনো পরিবর্তন হয় না। যা সাধারণ বিনিময় বিধি। |
গুণের সংযোগবিধি
আবার
যা গুণের সংযোগবিধি।
a, b, c যেকোনো তিনটি বীজগণিতীয় রাশির জন্য (ab)c=a (bc), যা গুণের সংযোগবিধি।
গুণের সূচকবিধি
আমরা জানি,
সাধারণভাবে যেখানে m, n যেকোনো স্বাভাবিক সংখ্যা।
এই প্রক্রিয়াকে গুণের সূচকবিধি বলা হয়।
আবার,
সাধারণভাবে,
গুণের বণ্টন বিধি
আমরা জানি,
= (a + a) + (b + b)
= 2a + 2b
আবার পাশের চিত্র হতে পাই,
ABEF আয়তক্ষেত্রটির ক্ষেত্রফল

= দৈর্ঘ্য প্রস্থ = BE AB=a2=2a=2a
আবার, ECDF আয়তক্ষেত্রটির ক্ষেত্রফল = দৈর্ঘ্য প্রস্থ
= ECCD=b2=2b= 2b
ABCD আয়তক্ষেত্রটির ক্ষেত্রফল
= ABEF আয়তক্ষেত্রের ক্ষেত্রফল + ECDF আয়তক্ষেত্রের ক্ষেত্রফল
= 2a + 2b
আবার, ABCD আয়তক্ষেত্রের ক্ষেত্রফল
= দৈর্ঘ্য প্রস্থ
= BC AB
= AB (BE + EC)
= 2 (a+b)
= 2(a + b)
2(a+b) =2a+2b.
| m(a+b+c+_______) = ma + mb + mc+ _________ এই নিয়মকে গুণের বণ্টনবিধি বলা হয়। |
আমরা জানি, 2 কে 4 বার নিলে 2 + 2 + 2 + 2 = 8 = 2 4 হয়। এখানে বলা যায় যে, 2 কে 4 দ্বারা গুণ করা হয়েছে।
অর্থাৎ, 2 4 = 2 + 2 + 2 + 2 = 8
যেকোনো বীজগণিতীয় রাশি a ও b এর জন্য
ab = ab _________ (i)
আবার
অর্থাৎ
সাধারণভাবে, __________ (ii)
আবার, গুণের বিনিময়বিধি
= - (b a)
= - (a b)
= - a b
অর্থাৎ, _____________ (iii)
আবার, [(iii) অনুযায়ী]
= - {- (ab)} [ (ii) অনুযায়ী]
= - (- ab)
= ab
অর্থাৎ, __________(iv)
লক্ষ করি :
দুটি একপদী রাশির গুণের ক্ষেত্রে তাদের সাংখ্যিক সহগদ্বয়কে চিহ্নযুক্ত সংখ্যার গুণের নিয়মে গুণ করতে হয়। উভয়পদে বিদ্যমান বীজগণিতীয় প্রতীকগুলোকে সূচক নিয়মে গুণ করে গুণফলে লিখতে হয়। অন্যান্য প্রতীকগুলো অপরিবর্তিত অবস্থায় গুণফলে নেওয়া হয়।
উদাহরণ ১। কে দ্বারা গুণ কর।
সমাধান:
[সূচক নিয়ম অনুযায়ী।
নির্ণেয় গুণফল
উদাহরণ ২। কে দ্বারা গুণ কর।
সমাধান:
নির্ণেয় গুণফল
উদাহরণ ৩। কে দ্বারা গুণ কর।
সমাধান:
নির্ণেয় গুণফল \
কাজ: ১। গুণ কর (ক) কে দ্বারা (খ) কে দ্বারা (গ) কে দ্বারা (ঘ) কে – 4abxy |
একের অধিক পদযুক্ত বীজগণিতীয় রাশিই বহুপদী রাশি। যেমন, একটি বহুপদী রাশি।
বহুপদী রাশিকে একপদী রাশি দ্বারা গুণ করতে হলে গুণ্যের (প্রথম রাশি) প্রত্যেক পদকে গুণক (দ্বিতীয় রাশি) দ্বারা গুণ করতে হয়।
উদাহরণ ৫। কে দ্বারা গুণ কর।
সমাধান:
নির্ণেয় গুণফল
উদাহরণ ৬। কে দ্বারা গুণ কর।
সমাধান:
কাজ: ১। প্রথম রাশিকে দ্বিতীয় রাশি দ্বারা গুণ কর: |
উদাহরণ ৮। 3x + 2y কে x + y দ্বারা গুণ কর।

গুণের নিয়ম:
উদাহরণ ৯। কে a - bদ্বারা গুণ কর।

উদাহরণ ১০। কে দ্বারা গুণ কর।

নির্ণেয় গুণফল
কাজ: ১ম রাশিকে ২য় রাশি দ্বারা গুণ কর। (ক) x + 7 , x + 9 (খ) (গ) |
১ম রাশিকে ২য় রাশি দ্বারা গুণ কর (১ থেকে ২৪)।
২। 5xy , 6az
১৩। 2a - 3b , 3a + 2b
১৪। a + b , a - b
২২। a + b + c , a + b + c
২৫। এবং B = x - y হলে, প্রমাণ কর যে,
২৬। এবং B = a + b হলে, AB = কত?
২৭। দেখাও যে,
২৮। দেখাও
ভাগের সূচক বিধি
= [লব ও হর থেকে সাধারণ উৎপাদক বর্জন করে]।
সাধারণভাবে, যেখানে m ও n স্বাভাবিক সংখ্যা এবং এই প্রক্রিয়াকে ভাগের সূচক বিধি বলা হয়।
লক্ষ করি:
a ≠ 0 হলে
আবার,
অনুসিদ্ধান্ত:
একপদী রাশিকে একপদী রাশি দ্বারা ভাগ করতে হলে, সাংখ্যিক সহগকে পাটিগণিতীয় নিয়মে ভাগ এবং বীজগণিতীয় প্রতীককে সূচক নিয়মে ভাগ করতে হয়।
উদাহরণ ১১। কে দ্বারা ভাগ কর।
সমাধান:
নির্ণেয় ভাগফল 2a3b4
উদাহরণ ১২। কে দ্বারা ভাগ কর।
সমাধান:
নির্ণেয় ভাগফল
উদাহরণ ১৩। কে দ্বারা ভাগ কর।
সমাধান: =
নির্ণেয় ভাগফল
কাজ: প্রথম রাশিকে দ্বিতীয় রাশি দ্বারা ভাগ কর। |
আমরা জানি, a+b+c একটি বহুপদী রাশি।
এখন
(a+b+c)÷d
=(a+b+c)
=a [গুণের বণ্টনবিধি]
=
আবার, ( a + b + c ) ÷ d
উদাহরণ ১৪। কে দ্বারা ভাগ কর।
সমাধান:
নির্ণেয় ভাগফল
কাজ: কে দ্বারা ভাগ কর। ২। কে দ্বারা ভাগ কর। |
বহুপদী রাশিকে বহুপদী রাশি দ্বারা ভাগ করার ক্ষেত্রে প্রথমে ভাজ্য ও ভাজক উভয়ের মধ্যে আছে এমন একটি বীজগণিতীয় প্রতীকের ঘাতের অধঃক্রম অনুসারে রাশিদ্বয়কে সাজাতে হবে। যেমন একটি বহুপদী। একে x এর মানের অধঃক্রম অনুসারে সাজালে আমরা পাই: এরপর পাটিগণিতের ভাগ প্রক্রিয়ার মতো নিচের নিয়মে ধাপে ধাপে ভাগ করতে হবে।
উদাহরণ ১৬। কে 2x - 1 দ্বারা ভাগ কর।
এখানে
এই 3.x দ্বারা ভাজক 2x+1 গুণ করে গুণফল ভাজ্যের সদৃশ পদের নিচে লিখে বিয়োগ করা হল: নতুন ভাজ্য 4x - 2 এর ক্ষেত্রে একই নিয়ম অনুসরণ করা হল
সমাধান:
এখানে ভাজ্য ও ভাজক উভয়েই x এর ঘাতের অধঃক্রম অনুসারে সাজানো আছে।

নির্ণেয় ভাগফল 3x+2
উদাহরণ ১৭। কে x - 2y দ্বারা ভাগ কর।
সমাধান: এখানে রাশি দুইটি x এর ঘাতের অধঃক্রম অনুসারে সাজানো আছে।

নির্ণেয় ভাগফল 2x + 3y
উদাহরণ ১৮। কে দ্বারা ভাগ কর।
সমাধান: এখানে রাশি দুটি x এর ঘাতের অধঃক্রম অনুসারে সাজানো আছে।

নির্ণেয় ভাগফল
মন্তব্য: ২য় ধাপে নতুন ভাজ্যকেও x এর ঘাতের অধঃক্রম অনুসারে সাজিয়ে লেখা হয়েছে।
উদাহরণ ১৯। কে দ্বারা ভাগ কর।
সমাধান: ভাজ্য ও ভাজক উভয়কে x এর ঘাতের অধঃক্রম অনুসারে সাজিয়ে পাই,
ভাজ্য =
ভাজক
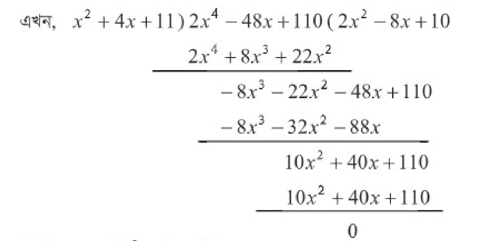
নির্ণেয় ভাগফল
উদাহরণ ২০। কে দ্বারা ভাগ কর।
সমাধান: এখানে রাশি দুটি x এর ঘাতের অধঃক্রম অনুসারে সাজানো আছে।

নির্ণেয় ভাগফল
কাজ: কে 2m - n দ্বারা ভাগ কর। কে দ্বারা ভাগ কর। কে দ্বারা ভাগ কর। |
একটি স্কুলের ম্যানেজিং কমিটি তাদের স্কুলের 10 জন গরীব শিক্ষার্থীর জন্য দুঃস্থ কল্যাণ তহবিল থেকে a টাকা বরাদ্দ করল। সেই টাকা থেকে প্রত্যেক শিক্ষার্থীকে প্রতিটি b টাকা মূল্যের 2 টি করে খাতা ও প্রতিটি c টাকা মূল্যের 1টি করে কলম বিতরণ করা হলো। এতে কিছু টাকা উদ্বৃত্ত হলো। এই টাকার সাথে আরও d টাকা যোগ করে তা 2 জন প্রতিবন্ধী শিক্ষার্থীর মধ্যে সমানভাবে ভাগ করে দেওয়া হলো।
উপরে বর্ণিত তথ্যগুলোকে বীজগণিতীয় রাশির মাধ্যমে প্রকাশ করতে পারি:
]
এখানে, ১ম বন্ধনী (), ২য় বন্ধনী {}, ৩য় বন্ধনী [] ব্যবহার করা হয়েছে। বন্ধনী স্থাপনের নিয়ম হচ্ছে [[()]]। এ ছাড়াও রাশিটিতে প্রক্রিয়া চিহ্ন,, ও ব্যবহার করা হয়েছে। এরূপ রাশির সরলীকরণে 'BEDMAS' (B for Braket, E for Exponent, D for Division, M for Multiplication, A for Addition. S for Subtraction) অনুসরণ করা হয়। আবার, বন্ধনীর ক্ষেত্রে পর্যায়ক্রমে ১ম, ২য় ও ৩য় বন্ধনীর কাজ করতে হয়।
বন্ধনী অপসারণ:
লক্ষ করি: b > c
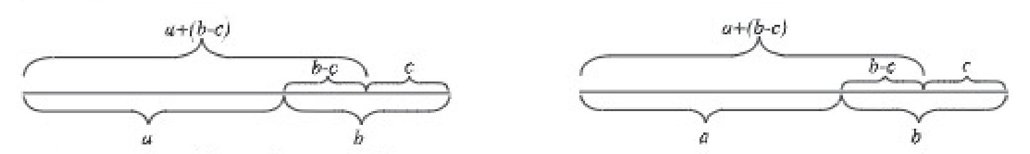
চিত্রে দেখা যায়, a + (b - c) = a + b - c
| বন্ধনীর আগে '+' চিহ্ন থাকলে, বন্ধনী অপসারণে বন্ধনীর ভিতরের পদগুলোর চিহ্নের পরিবর্তন হয় না। |
আবার, লক্ষ করি: b > c a > b - c


চিত্রে দেখা যায়, a - (b - c) = a - b + c
লক্ষ করি: a - (b - c) + (b - c) = a
আবার, a - b + c + (b - c) = a
সুতরাং, a - (b - c) = a - b + c
[ - (b - c) এর যোগাত্মক বিপরীত (b - c) ]
| বন্ধনীর আগে'-' চিহ্ন থাকলে, বন্ধনী অপসারণে বন্ধনীর ভিতরের পদগুলোর চিহ্নের পরিবর্তন হয়ে বিপরীত চিহ্নযুক্ত হয়। |
| কাজ: নিচের রাশিগুলোর বন্ধনী অপসারণ কর। | |
| বন্ধনীযুক্ত রাশি | বন্ধনীমুক্ত রাশি |
| 8+(6-2) | |
| 8-(6-2) | 8-6+2 |
| p+q+(r-s) | |
| p+q-(r-s) | |
| কাজ: নিচের রাশিগুলোর মান অপরিবর্তিত রেখে বন্ধনী স্থাপন কর। | |||
| রাশি | বন্ধনীর আগের চিহ্ন | বন্ধনীর অবস্থান | বন্ধনীযুক্ত রাশি |
| 7+5-2 | + | ২য় ও ৩য় পদ ১ম বন্ধনীভুক্ত অর্থাৎ, (5-2) | 7+(5-2) |
| 7-5+2 | - | ২য় ও ৩য় পদ ১ম বন্ধনীভুক্ত অর্থাৎ (-5 + 2) | 7-(5-2) |
| a-b+c-d | + | ৩য় ও ৪র্থ পদ ১ম বন্ধনীভুক্ত | |
| a-b-c-d | - | ||
উদাহরণ ২১। সরল কর 6 - 2{5 - (8 - 3) + (5 + 2)}
সমাধান:
6 - 2{5 - (8 - 3) + (5 + 2)}
= 6 - 2{5 - 5 + 7}
= 6 - 2{7}
=6-14
=-8
উদাহরণ ২২। সরল কর: a+ b - (c - d)
সমাধান:
a + {b - (c - d)}
= a + {b - c + d}
= a + b - c + d
উদাহরণ ২৩। সরল কর: a - [b - {c - (d - e)} - f]
সমাধান:
a - [b - {c - (d - e)} - f]
= a - [b - {c - d + e} - f]
= a - [b - c + d - e - f]
= a - b + c - d + e + f
উদাহরণ ২৪। সরল কর 3x - [5y - {10z - (5x - 10y + 3z)}]
সমাধান:
3x - [5y - {10z - (5x - 10y + 3z)}]
= 3x - [5y - {10z - 5x + 10y - 3z}]
= 3x - [5y - {7z - 5x + 10y}]
= 3x - [5y - 7z + 5x - 10y]
= 3x - [5x - 5y - 7z]
= 3x - 5x + 5y + 7z
= - 2x + 5y + 7z
= 5y - 2x + 7z
উদাহরণ ২৫। 3x - 4y - 8z + 5 এর তৃতীয় ও চতুর্থ পদ বন্ধনীর আগে (-) চিহ্ন দিয়ে প্রথম বন্ধনীভুক্ত কর। পরবর্তীতে দ্বিতীয় পদ ও প্রথম বন্ধনীভুক্ত রাশিকে দ্বিতীয় বন্ধনীভুক্ত কর যেন বন্ধনীর আগে (-) চিহ্ন থাকে।
সমাধান:
3x - 4y - 8z + 5 রাশিটির তৃতীয় ও চতুর্থ পদ যথাক্রমে ৪৫ ও 5 প্রশ্নানুসারে, 3x - 4y - (8z - 5) আবার, 3x - {4y + (8z - 5)}
কাজ: সরল কর: 1 . x - {2x - (3y - 4x + 2y)} 2 . 8x + y - [7x - {5x - (4x - 3x - y) + 2y}] |
১। 3a2b এবং -4ab2 এর গুণফল নিচের কোনটি?
(ক) - 12a2b2
(খ) -12a3b2
(গ) -12a2b3
(ঘ) - 12a3b3
২। 20a6b3 কে দ্বারা ভাগ করলে ভাগফল নিচের কোনটি?
৩। = কত?
8 a=3,b=2 হলে, (8a2b)+(-7a+4b) এর মান কত?
ক) 3
(খ) 4
(গ) 7
(ঘ) 15
৫ । x = - 1 হলে, এর মান নিচের কোনটি?
(ক) -4
(খ)-2
(গ) ০
(ঘ) 2
কে দ্বারা ভাগ করলে ভাগফল কত হবে?
৭। একটি বীজগণিতীয় রাশি।
(i) বহুপদী রাশিটির চলক a
(ii) বহুপদীটির মাত্রা 4
(iii) এর সহগ 6
নিচের কোনটি সঠিক?
(ক) i ও ii
(খ) ii ও iii
(গ) i ও iii
(ঘ) i, ii ও iii
৮। x = 3, y = 2 হলে এর মান কত?
৯। হলে, a০ এর মান কত?
(ক) 0
(খ) a
(গ) 1
(ঘ)
১০। = কতো ?
নিচের তথ্যের আলোকে ১১-১২ নং প্রশ্নের উত্তর দাও।
দুটি বীজগণিতীয় রাশি x + y এবং x - {x - (x - y)}
১১। দ্বিতীয় রাশির মান নিচের কোনটি?
(ক) x + y
(খ) - x - y
(গ) x - y
(ঘ)
১২। রাশি দুটির গুণফল নিচের কোনটি?
(ক)
(খ)
(গ) x - y
(ঘ)
১৩। = কতো ?
১৪। [2 - {(1 + 1) - 2}] এর সরলফল কত?
(ক) -4
(খ) 2
(গ) 4
(ঘ) 0
সরল কর (১৫ থেকে ২৯):
১৫। 7 + 2[- 8 - {- 3 - (- 2 - 3)} - 4]
১৬। - 5 - [- 8 - {- 4 - (- 2 - 3)} + 13]
১৭। 7 - 2[- 6 + 3{- 5 + 2(4 - 3)}]
১৮। x - {a + (y - b)}
১৯। 3x + (4y - z) - {a - b - (2c - 4a) - 5a}
২০। - a + [- 5b - {- 9c + (- 3a - 7b + 11c)}]
২১। - a - [- 3b - {- 2a - (- a - 4b)}]
২২। {2a - (3b - 5c)} - [a - {2b - (c - 4a)} - 7c]
২৩। - a + [- 6b - {- 15c + (- 3a - 9b - 13c)}]
২৪। - 2x - [- 4y - {- 6z - (8x - 10y + 12z)}]
২৫। 3x - 5y + [2 + (3y - x) + {2x - (x - 2y)}]
২৬। 4x + [- 5y - {9z + (3x - 7y + x)}]
২৭। 20 - [{(6a + 3b) - (5a - 2b)} + 6]
২৮। 15a + 2[3b + 3{2a - 2(2a + b)}]
২৯। [8b - 3{2a - 3(2b + 5) - 5(b - 3)}] - 3b
৩০ বন্ধনীর পূর্বে (-) চিহ্ন দিয়ে a - b + c - d এর ২য়, ৩য় ও ৪র্থ পদ প্রথম বন্ধনীর ভিতর স্থাপন কর।
৩১। a - b - c + d - m + n - x + y রাশিতে বন্ধনীর আগে (-) চিহ্ন দিয়ে ২য়, ৩য় ও ৪র্থ পদ ও (+) চিহ্ন দিয়ে ৬ষ্ঠ ও ৭ম পদ প্রথম বন্ধনীভুক্ত কর।
৩২। 7x - 5y + 8z - 9 এর তৃতীয় ও চতুর্থ পদ বন্ধনীর আগে (-) চিহ্ন দিয়ে প্রথম বন্ধনীভুক্ত কর। পরে দ্বিতীয় পদ ও প্রথম বন্ধনীভুক্ত রাশিকে দ্বিতীয় বন্ধনীভুক্ত কর যেন বন্ধনীর আগে (+) চিহ্ন থাকে।
৩৩। এবং 5x - 1 দুটি বীজগণিতীয় রাশি।
ক. প্রথম রাশি থেকে দ্বিতীয় রাশি বিয়োগ কর।
খ. রাশিদ্বয়ের গুণফল নির্ণয় কর।
গ. প্রথম রাশিকে দ্বিতীয় রাশি দ্বারা ভাগ কর।
৩৪। এবং
ক) A - B = কত?
খ) A ও B এর গুণফল নির্ণয় কর।
গ) নির্ণয় কর।
আমরা জানি,
সুতরাং
একইভাবে,
লক্ষ করি:

common.read_more